I'm still working on a new entry for Game Restart, but I wanted to pass along something I've been learning about rolling up characters on an 8-bit home computer from the 80s.
Computers from the 1980s running BASIC had a dedicated command for generated random numbers within the course of running a program. And this is what I, a teenaged neophyte without any real exposure to statistics or how random numbers ought to be handled, would have used without question, without any real testing. Computers might be seen as final arbiters when it comes to—well, computing anything—so why would I think to question the RND command?
In 1984 or 1985, this would have been sufficient for anything and everything I would have done with my Commodore 128 (the computer I spent significant personal time with from 1985 to 1989). After all, I'm just rolling up a character for a fantasy RPG. The question of fairness might not even have occured to me — though obviously the fact that rolling dice is fun, it would be therefore preferable on that basis alone, if I didn't have to do it a lot, because tallying dice totals might get a little tedious after a few rounds of stats, which is why I might want a computer to do the tedious part, since the really fun parts of rolling up characters is their names and backstories (some of us may have taken the role part of the play more seriously than necessary).
I believe I've just described a level of naïveté possibly expected from a teenager with aspirations of creating a useful utility to assist with a pastime normally spent with friends, but which could only be made by sitting alone in a bedroom with a computer and a used black-and-white television set.
So on numerous occasions this was a problem I attempted to solve with a computer, probably because I didn't necessarily have that many friends, and … because I liked playing on the computer. A natural mashup of interests. RPGs gave me an excuse to use the computer in ways which had nothing to do with electronic games.
If I had a better background in statistics, I might have tested — or at least doubted — the abilities of the computer to generate random numbers by default. But as it turns out, the Commodore is apprently not capable by default of generating random numbers as well as rolling real dice.
I am not a programmer. Once BASIC fell out of vogue, my interaction with most computers was pushed into using applications, helped in no small part by my new interest in a career in graphic design.
So what was I seeing? Weird results: normally 3d6 generates numbers from three to 18, with distribution along the lines of a bell curve: threes and 18s should be much less frequent than tens or elevens. But with my barely-remembered hunt-and-pecking of BASIC, I wouldn't get any characters that rolled fours or 17s in their abilities stats. At all. I started to wonder about the results of my intitial take, if the results of a character-rolling on the computer was sufficiently fair for the purposes of role-playing gaming. And that's when I started reading about some things. and possible ways to address what I was seeing with my naive approach to using RND to generate random numbers.
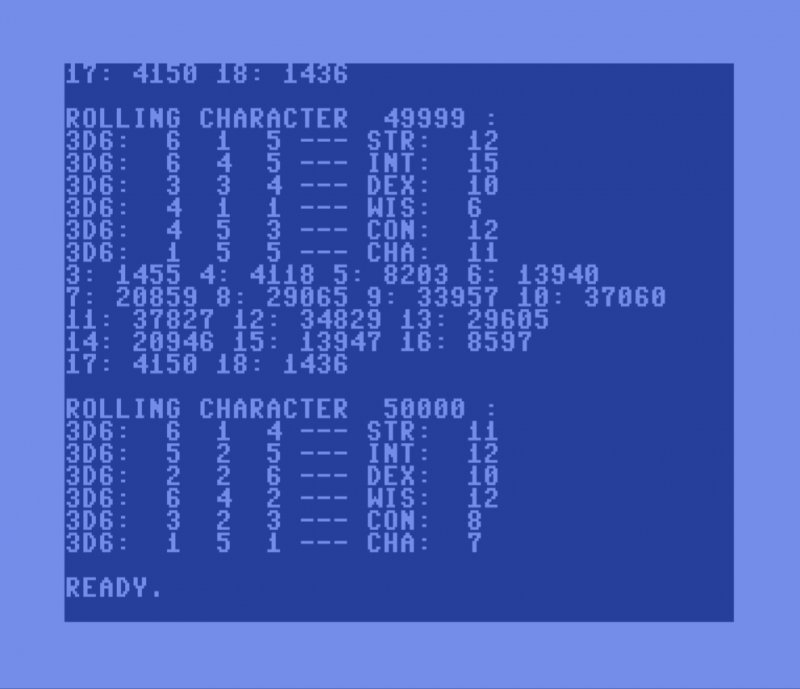
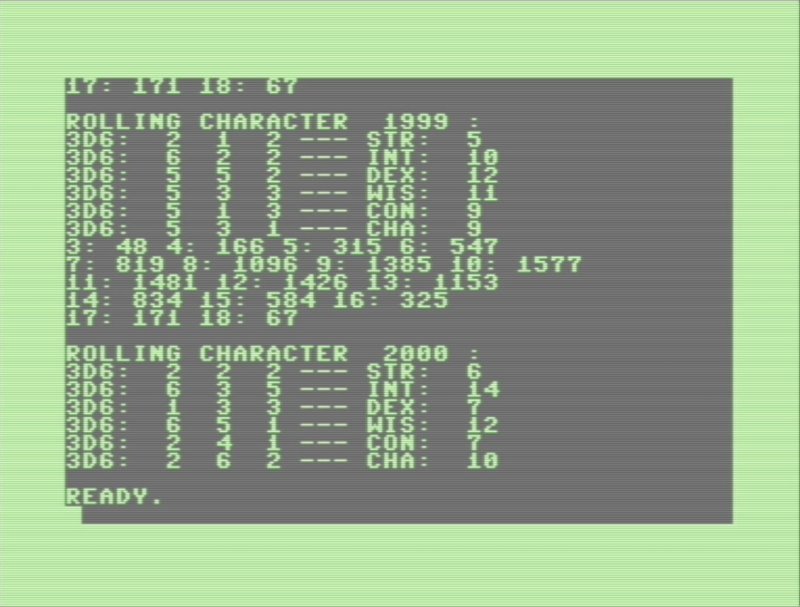
Finally I thought I had the breakthrough I think I needed. I'd written some BASIC to sort of count the number of times a given result of randomly emulating a 3d6 roll, then made the VICE x64 emulator run this in Warp mode for several sessions for 10,000-20,000 game characters each (so 60,000-120,000 "rolls," since each character has six ability scores). No idea if this would be statistically significant, but I think it satisfactory for the purpose of a blog post on rolling up about two dozen non-player characters for a table-top role-playing game scenario:
3: 1455
4: 4118
5: 8203
6: 13940
7: 20859
8: 29065
9: 33957
10: 37060
11: 37827
12: 34829
13: 29605
14: 20946
15: 13947
16: 8597
17: 4150
18: 1436That looks basically like a bell curve to me, and comes with a small jolt of serotonin. Hey, I'll take it!
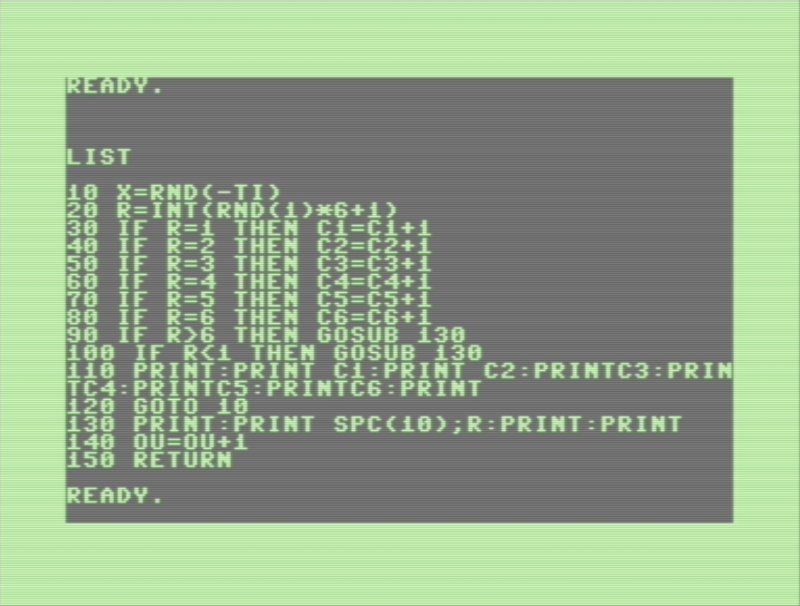
First, I needed to reseed the random number generation, using the internal clock counter of the Commodore (question marks are shortcuts for PRINT):
10 x=rnd(-ti): rem 1d6 randomness testing-am I doing this right?
20 r=int(rnd(1)*6+1)
30 if r=1 then c1=c1+1
40 if r=2 then c2=c2+1
50 if r=3 then c3=c3+1
60 if r=4 then c4=c4+1
70 if r=5 then c5=c5+1
80 if r=6 then c6=c6+1
90 if r>6 then gosub 130
100 if r<1 then gosub 130
110 ?:? c1:? c2:? c3:? c4:? c5:? c6:?
120 goto 10
130 ?:? spc(10);r:?:?
140 ou=ou+1
150 return
I ran this for quite a while, and while the values of the "die rolls" never equalized, it did seem an acceptable way to modify my character-roller program. So uncertain I was of my ability to do the thing properly, I inserted probably unnecessary subroutines for dealing with under- and overages in the number generation.
I thought things worked well enough, so I finished it off:
10 rem d&d/ad&d character attributes
20 rem randomizer/generator
30 rem
40 rem s = str, i = int, d = dex, w = wis, c = con, ch= chas, c = con, ch= cha
50 r3=0:r4=0:r5=0:r6=0:r7=0:r8=0:r9=0:ra=0
60 rb=0:rc=0:rd=0:re=0:rf=0:rg=0:rh=0:ri=0
70 print chr$(147)
80 x=rnd(-ti) : rem seed generation for rnd calls
90 input "how many characters do you wish to roll up";h
100 for hr = 1 to h
110 d1=0:d2=0:d3=0
120 print"rolling character ";hr; ": " "
130 for dx=1 to 6 :read ca$
140 let x=1
150 d1=int(rnd(x)*6+1)
160 d2=int(rnd(x)*6+1)
170 d3=int(rnd(x)*6+1)
180 print "3d6: "; d1; d2; d3;
190 let dt=d1+d2+d3
200 if dt=3 then r3=r3+1 : rem incrementers for determining distribution
210 if dt=4 then r4=r4+1 : rem (should be a symmetrical bell curve!)
220 if dt=5 then r5=r5+1
230 if dt=6 then r6=r6+1
240 if dt=7 then r7=r7+1
250 if dt=8 then r8=r8+1
260 if dt=9 then r9=r9+1
270 if dt=10 then ra=ra+1
280 if dt=11 then rb=rb+1
290 if dt=12 then rc=rc+1
300 if dt=13 then rd=rd+1
310 if dt=14 then re=re+1
320 if dt=15 then rf=rf+1
330 if dt=16 then rg=rg+1
340 if dt=17 then rh=rh+1
350 if dt=18 then ri=ri+1
360 if dx=1 then let s=dt
370 if dx=1 then print "--- ";ca$;": ";dt
380 if dx=2 then let i=dt
390 if dx=2 then print "--- ";ca$;": ";dt
400 if dx=3 then let d=dt
410 if dx=3 then print "--- ";ca$;": ";dt
420 if dx=4 then let w=dt
430 if dx=4 then print "--- ";ca$;": ";dt
440 if dx=5 then let c=dt
450 if dx=5 then print "--- ";ca$;": ";dt
460 if dx=6 then let ch=dt
470 if dx=6 then print "--- ";ca$;": ";dt
480 next dx
490 if h=hr then end
500 s=0:i=0:d=0:w=0:c=0:ch=0:dx=0:restore:rem reset vars/pointer
510 print "3:";r3;"4:";r4;"5:";r5;"6:";r6
520 print "7:";r7;"8:";r8;"9:";r9;"10:";ra
530 print "11:";rb;"12:";rc;"13:";rd
540 print "14:";re;"15:";rf;"16:";rg
550 print "17:";rh;"18:";ri:print
560 next hr
570 data "str","int","dex","wis","con","cha"
It's interesting that this program is more complex than the final version, which I'll share later.
For the record, I focused on the 64 version because VICE is much faster at emulating the C64 than it is the Commodore 128 on my machine, but I did test the code a bit on the C128:
I did not, however, run as many iterations on the C128 as I did on the C64.